고정 헤더 영역
상세 컨텐츠
본문
(1) 황금분할
모든 길이는 황금비율로 나누었을 때,
짧은 것 : 긴 것 = 긴 것 : 전체의 관계가 성립합니다.
이러한 관계를 황금분할이라 하는데, 프렉탈의 원리가 녹아있는 걸 알 수 있습니다.

전체 길이를 1로 보면, 분할된 비율은 0.382 : 0.618이 되며, 이는 0.618 : 1과 같습니다.
즉, 0.382 ÷ 0.618 = 0.618 ÷ 1 = 0.618 로서 황금비율인 것이죠.
(2) 황금 직사각형
두 변이 황금비율을 이루는 직사각형을 가리켜 황금 직사각형이라 부르는데요.
황금비율을 X 축인 수직선상에 구현한 것이 황금분할이라면,
황금비율을 X, Y라는 두 개의 축 위에 구현한 것은 황금 직사각형입니다.
즉, 이 둘은 각각 1차원과 2차원에서 황금비율을 구현한 것이죠.

황금 직사각형에서 긴 변과 짧은 변은 1.618 대 1의 비율을 이룹니다.
황금 직사각형을 그리려면 그림 21-2처럼 먼저 가로 세로 2 단위의 정사각형을 그린 다음,
밑변의 중점 E에서 맞은편 모서리 B에 선을 그어야 합니다.
그런 다음 중점 E를 중심으로 원주를 그리면 밑변 EG가 되고, 황금 직사각형 AFGC가 완성되는 것이죠.

위 그림에서 복잡한 수식은 그냥 재끼셔도 됩니다.
다음 결론만 이해하세요.
AFGC는 CG : FG = 1.618 : 1
BFGD는 FG : DG = 1.618 : 1 ( 또는 DG : FG = 0.618 : 1 )
이 되어 둘 다 황금 직사각형을 이룹니다.
(3) 황금 나선형
황금분할과 황금 직사각형이 파동의 정적인 형태를 나타낸다면,
역동적인 형태를 나타내는 것은 황금 나선형입니다.
회오리바람을 떠올리시면, 3차원적 움직임이라고 볼 수 있겠죠.
황금 나선형은 황금 직사각형이 나선형으로 확장되는 프렉탈 패턴입니다.

모든 황금 직사각형은 정사각형과 작은 황금 직사각형으로 나누어지며,
이론적으로 이 분할은 무한대로 계속할 수 있습니다.
정사각형 A, B, C, D, E, F, G가 나선형으로 회전하는 패턴이 보이시죠?
이를 파동에 적용해보면, 다음과 같은 그림이 됩니다.
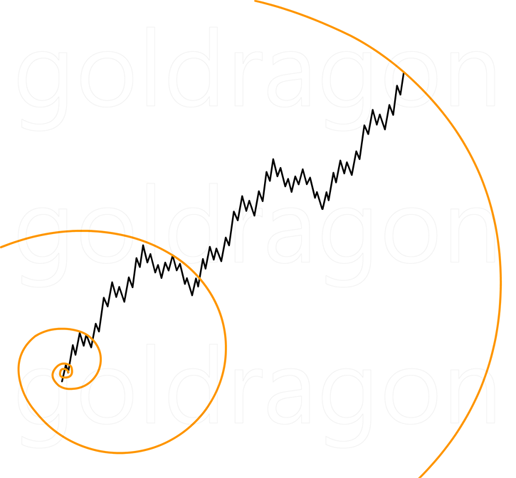


황금 나선형의 모든 부분에서 호의 길이와 지름의 비율은 1대 1.618이 됩니다.
그림에서 arc는 호의 길이를 의미하는데,
호 WX, XY, YZ는 붉은 나선을 이루고 있는 걸 볼 수 있습니다.
또한, 지름과 반지름 그리고 지름과 직각으로 떨어진 반지름 사이의 비율도 1.618이 됩니다.
가령, 지름 d₁(=r₁ + r₃)을 반지름 r₃로 나누면 1.618이고,
지름 d₂(=r₂ + r₄)를 직각으로 떨어진 반지름 r₃로 나누면 역시 1.618이 나오는 걸 알 수 있습니다.
오늘은 황금비율에서 파생된 3가지 개념에 대해 정리했습니다.
다음 포스팅을 끝으로, 피보나치 수열의 이론 파트는 마무리가 될 듯합니다.
책에서 사족이 되는 부분은 최대한 걸러냈음에도 불구하고
지루한 감이 있네요.
피보나치 수열의 기본적인 사항을 정리했다는 것에 의미를 두시기 바랍니다.

'엘리어트 파동이론' 카테고리의 다른 글
| 23. 동인 파동의 비율 관계 (0) | 2022.06.13 |
|---|---|
| 22. 수열과 파동 (0) | 2022.06.04 |
| 20. 수열의 진행 방향 (1) | 2022.06.04 |
| 19. 피보나치 수열 (2) | 2022.05.29 |
| 18. 척도 (4) | 2022.01.13 |





댓글 영역